HyperSHAP: Opening the Black Box of Hyperparameter Optimization with Explainable AI

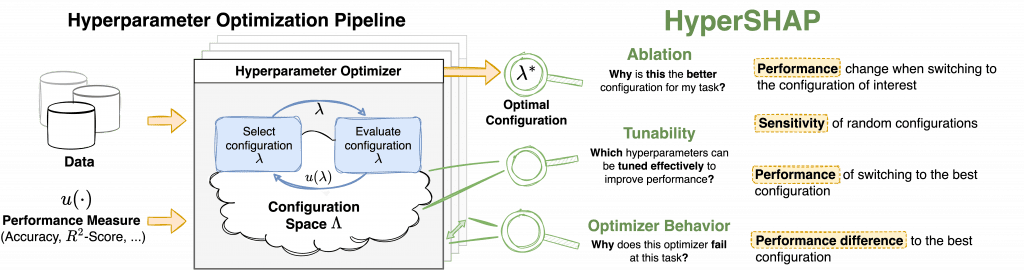
Which value of a hyperparameter configuration was doing the trick? Why does tuning optimizer momentum help only when weight decay is tuned as well? And why does the optimizer keep “missing” the best configuration?

These are the kinds of questions every machine learning practitioner eventually asks, and often struggles to answer. Hyperparameter optimization (HPO) delivers strong performance, but usually at the cost of transparency. The recent paper “HyperSHAP: Shapley Values and Interactions for Explaining Hyperparameter Optimization” (Wever et al., 2026) tackles this in a principled way providing a unifying framework for explaining HPO from different angles.

In this post, we will unpack what HyperSHAP is, why it matters, and how it could change the way we understand and trust AutoML systems.

Why Explaining Hyperparameter Optimization Matters

Hyperparameter tuning is everywhere. From classical tabular machine learning models to deep learning architectures to large language models, performance often depends more on tuning than on the base algorithm itself. Sophisticated HPO methods now routinely explore thousands of configurations for us. But there is a problem:

We get better models, but worse understanding.

Most HPO tools behave like black boxes. They return a “best” hyperparameter configuration without informing us about:

• Which hyperparameters really mattered
• Which ones interacted
• Which ones were wasted effort
• Whether the optimizer made systematic mistakes

In safety-critical, high-cost, or scientific settings, this lack of transparency limits trust and adoption. Researchers and practitioners want more than good numbers: they want explanations. HyperSHAP addresses exactly this gap.

HyperSHAP: The Basic Idea and Framework

At the heart of the paper is a simple but powerful question:

How can we explain why certain hyperparameters and combinations thereof lead to better performance?

More concretely:

• Can we attribute performance gains to individual hyperparameters?
• Can we detect interactions between them?
• Can we analyze whether an optimizer exploits these effects well?
• Can we turn these explanations into actionable insights?

Existing methods, like fANOVA (Hutter et al., 2014) and Local Parameter Importance (Biedenkapp et al., 2017), partially answer these questions, but they focus mostly on variance and ignore tunability or deeper interactions. HyperSHAP proposes a unified, game-theoretic framework to fill this gap.

If you are familiar with explainable AI, you have probably seen Shapley values used for feature attribute: “This feature contributed +0.3 to the prediction.” HyperSHAP adapts this idea to hyperparameters.

Think of hyperparameters as players in a cooperative game:

• The “reward” is model performance
• Each player contributes by being tuned
• Players can cooperate (interact) or conflict

The goal is then to fairly divide credit for performance among them. This is exactly what Shapley values from game theory were designed to do. HyperSHAP extends this idea to multiple settings in HPO.

HyperSHAP defines several explanation games, each answering a different practical question:

1. Ablation: Why is this hyperparameter configuration better?
   This considers contributions of individual hyperparameter values and their interactions.
2. Sensitivity: Which hyperparameters cause variability?
   This connects HyperSHAP to classical variance-based methods and fANOVA.
3. Tunability: Which hyperparameters are worth tuning?
   Instead of measuring variance, this game quantifies how much tuning a hyperparameter can improve model performance.
4. Optimizer Bias: Where does my optimizer fail?
   This game helps to detect systematic blind spots of optimizers, e.g., whether they fail to exploit certain hyperparameters or acknowledge interaction effects.

Try HyperSHAP Today

HyperSHAP is not just a theoretical framework but ready to explain HPO to you as a Python package:

$ pip install hypershap

Furthermore, the implementation of HyperSHAP is open source and can be found on GitHub. The full paper with technical appendix can be found on arXiv.

Starting from a ConfigSpace object describing the hyperparameter space and a blackbox_function mapping hyperparameter configurations to real-valued performance values, the HyperSHAP package allows to create plots within 3 lines of code:

from hypershap import ExplanationTask, HyperSHAP

# Instantiate HyperSHAP
hypershap = HyperSHAP(ExplanationTask.from_function(config_space=cs, function=blackbox_function))

# Run tunability analysis
hypershap.tunability(baseline_config=cs.get_default_configuration())

# Plot results as a Shapley Interaction graph
hypershap.plot_si_graph()

For an instance of the PD1 benchmark the resulting plot could look like this:

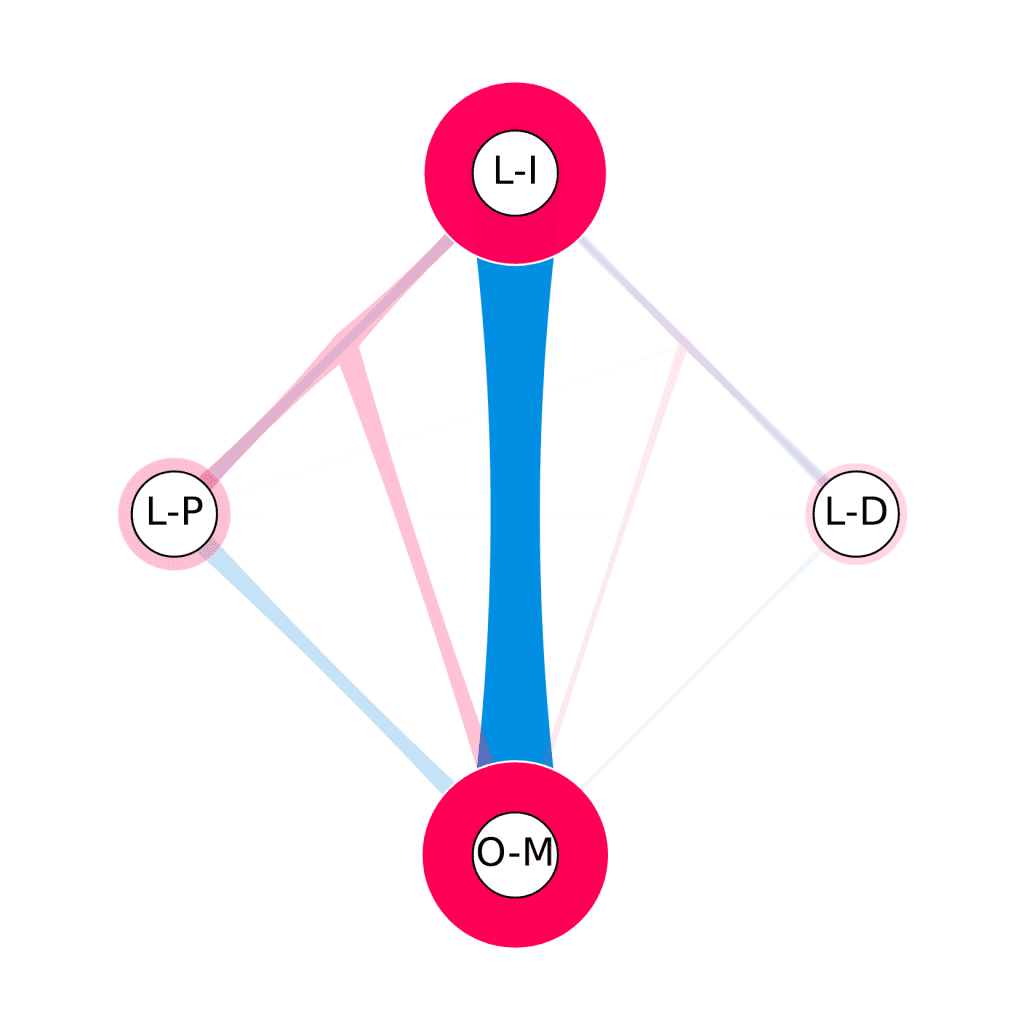
Positive contributions of hyperparameters (or interactions between hyperparameters) are indicated by red color whereas negative contributions or interactions are indicated by blue color. In this example, we have four hyperparameters: initial learning rate (L-I), optimizer momentum (O-M), learning rate decay factor (L-D), learning rate power (L-P). We can observe that L-I and O-M are the two most important hyperparameters according to their main effects represented by circles around the hyperparameter nodes. However, their interaction, visualized in terms of hyperedges, is highly negative, showing that tuning both simulateneously is highly redundant. Intuitively, this makes sense as setting the initial learning rate properly for a task works well with the standard optimizer momentum and vice versa: If the optimizer momentum is tailored to the task, the initial learning rate does not need to be tuned exactly.

References

Hutter, F., Hoos, H., & Leyton-Brown, K. (2014, January). An efficient approach for assessing hyperparameter importance. In International conference on machine learning (pp. 754-762). PMLR.

Biedenkapp, A., Lindauer, M., Eggensperger, K., Hutter, F., Fawcett, C., & Hoos, H. (2017, February). Efficient parameter importance analysis via ablation with surrogates. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 31, No. 1).

Wever, M., Muschalik, M., Fumagalli, F., & Lindauer, M. (2026). HyperSHAP: Shapley Values and Interactions for Hyperparameter Importance. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 40).