Towards Token-Level Hybrid Attention Architectures

The softmax attention models have become a keystone in modern large language models (LLMs). However, the quadratic computational and linear memory complexities have gradually become bottlenecks in the long term. In the meantime, recent advances in linear attention models have provided another promising direction for more efficient attention models. Linear attention replaces the non-linear softmax operations in transformers with linear variations. And therefore, allow merging the past KV values into a single hidden state. Nevertheless, it remains unclear whether a single hidden state can retain all the past context required for future queries. 

In this blog post, we introduce Neural Attention Search Linear (NAtS-L), a framework that automatically determines whether a token should be processed with linear attention (i.e., tokens with only short-term impact) or softmax attention (i.e., tokens containing information related to long-term retrieval). We show that this attention operation type information can be learned jointly with architecture weights, yielding both efficient and strong-performing architectures. 

Background: Linear Attention vs. Softmax Attention

In attention models, the input hidden states are first mapped into three matrices: Q , K, and V. The attention operation then outputs the weighted sum of V by computing the correlation between Q and K with certain functions.

$\mathbf{O} = f(\mathbf{Q} \mathbf{K}^{T}, \mathbf{M})\mathbf{V}$

Where $f$ is a function that transforms the attention map $\mathbf{Q} \mathbf{K}^{T}$ to improve its expressibility, and M is an attention mask that controls whether one token should be correlated with another token. If we treat $f$ softmax, we return to the non-linear softmax attention operation. However, if we use $f$ as a kernel function, we could also first merge $\mathbf{K}^T\mathbf{V}$ into one hidden state and then compute the output by multiplying $\mathbf{Q}$ with this hidden state:

$\mathbf{s}_{t} = g(\mathbf{k}_{0,1…t}, \mathbf{v}_{0,1,…t})$

$\mathbf{o}_t = \mathbf{q}_t\mathbf{s}_t$

Hence, linear attention only requires linear computational complexity during the pre-filling stage and constant complexity during decoding. Additionally, the linear attention models only require a fixed hidden state to store all the previous information. However, a single hidden state with a fixed size might not be able to store all historical information over a long context. 

Method: Searching for the optimal Operation Type for each Token

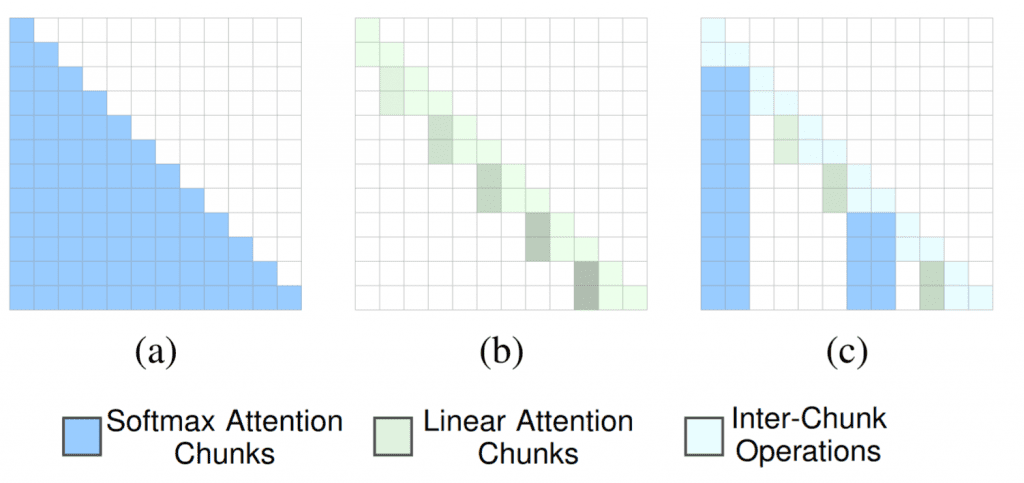
Given that linear attention is better at dropping unimportant information, while softmax attention can preserve information for long-term context modeling, we could combine both operations at the same level and ask the model to adaptively decide whether a token should be processed with linear or softmax attention. We consider this decision process as a neural architecture search problem. The model will learn to search for the optimal operation type for each token within the input sequence. 

For computational efficiency, instead of checking the operation type for each token, we group multiple tokens into a single chunk and determine the type of each chunk, avoiding fragmented computation. More specifically, we apply average pooling followed by a linear layer that maps each chunk to a set of scores, and select the operations with the highest scores for each chunk. The gradient for the scoring layer can be computed jointly with the model weights. Therefore, the model will automatically determine the optimal attention operation type for each token. 

We evaluate NAtS-L across different benchmarking tasks, showing that it achieves better long-context retrieval performance than both non-linear softmax attention models and linear attention models. This provides a promising direction towards hybrid attention models.

For detailed information, please check the paper: Neural Attention Search Linear: Towards Adaptive Token-Level Hybrid Attention Models