Submitted by Collin Coil and Nick Cheney as part of the AutoML’25 conference
Freezing layers in deep neural networks seems counterintuitive. Why would training less of a network lead to faster convergence and better generalization? To our knowledge, no empirical work has been done to explain how freezing layers produces these two benefits. Some prior works on freezing layers have used Cover’s theorem as a theoretical justification. This theorem states that random nonlinear transformations into equal or higher dimensions increase the probability that data points are linearly separable.
For an intuitive example, imagine a 2D chessboard. It’s impossible to draw a plane separating the black and white squares. However, if we randomly project the squares into higher dimensions, we’re practically guaranteed to find a way to separate the squares. Many machine learning methods rely on dimensional tricks like this. According to the conventional wisdom, neural networks with frozen layers a similar trick to find solutions.
We put that theory to the test. Using multilayer perceptrons (MLPs), we empirically examined whether freezing layers increases linear separability, and more importantly, whether that separability translates into better performance. We call these partially frozen models “reservoir networks,” drawing from reservoir computing in RNNs. Our results suggest that while separability is higher in some reservoir networks, the connection to better generalization is neither direct nor universal. As a result, we claim that explanations of freezing’s benefits using Cover’s theorem are insufficient.
What Is Freezing, and What Actually Happens When You Freeze
To freeze a layer, we prevent its weights from updating at any point during training, and we freeze several layers at regular intervals throughout the network. These weights still affect both forward and backward passes, but they remain fixed at their random initialization.
We trained MLPs across a range of conditions, using both fully trainable and reservoir networks. We assessed linear separability of the hidden states at each layer of the network using a linear probe. Freezing layers consistently improved generalization and linear separability scores on CIFAR-10 and CIFAR-100, but only in networks with significant overparameterization. Narrower networks, shallower networks, or those trained on MNIST showed diminished or negative returns. Other architectural features, such as skip connections or position of the frozen layers, substantially impacted the feature dynamics. Cover’s theorem provides no theoretical backing to explain why these architectural choices interact with freezing, so explanations relying solely on the theorem are insufficient.
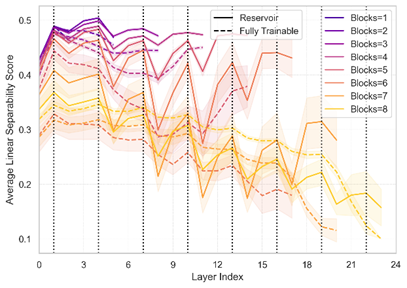
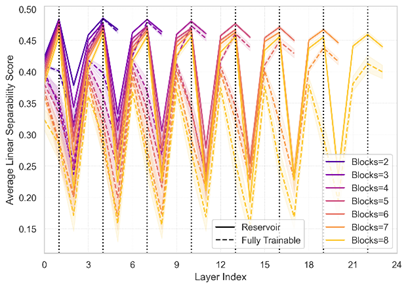
Linear separability scores of networks trained on CIFAR-10 for reservoir and fully trainable networks without (left) and with (right) skip connections. Vertical black lines signify frozen layers in reservoir networks. Architectural choices, such as including skip connections, substantially alter the impacts of freezing layers.
Beyond accuracy, reservoir networks also converged faster. Interestingly, similar speedups occurred even when we randomly froze a subset of weights within layers. In this situation, some weights are updated, producing partially random transformations that violate Cover’s assumptions. The fact that we see similar behavior in reservoir networks and networks with randomly frozen weights is further evidence that Cover’s theorem is insufficient. Instead, it hints at a deeper mechanism. We hypothesize that freezing smooths the optimization landscape and acts as a form of regularization.
Rethinking Freezing as a Design Choice
Most practitioners treat freezing as a training trick, useful for transfer learning or accelerating convergence. Our findings suggest it should be thought of as an architectural decision. The number of frozen layers, their placement, width, and whether layers are partially or fully frozen all significantly alter the model’s performance. This opens up a new axis in neural architecture search. Our results suggest that in some regimes, strategic freezing can improve performance with less compute and shorter training times.
Where to Go from Here
Our study leaves several open questions. First, how do these results generalize to other architectures like CNNs or transformers? Second, can we formally quantify the smoothing effect of freezing on the loss surface? And third, how can we best incorporate freezing into NAS frameworks to discover architectures that are both efficient and performant?
Cover’s theorem gave us an elegant story for why freezing layers helps. But the real picture is messier and more interesting. Freezing appears to work not because of how it transforms features, but because of how it reshapes the optimization landscape and constrains overfitting. By reframing freezing as an architectural tool, we open new paths for building models that are easier to train and better performing.

Comments are closed