We set out to understand: How exactly does prior informativeness translate into lower sample complexity? And how can we exploit that safely in practice?

Reframing HPO Through the Lens of ϵ-Best-Arm Identification

To answer these questions, we model HPO as a fixed-budget ϵ-Best-Arm Identification (BAI) problem. Each configuration becomes an arm with an unknown full-fidelity mean, observed through noisy, cheaper, lower-fidelity signals.
We explicitly introduce Bayesian priors over arm means, which allows us to reason about how near to optimal a configuration is before performing any evaluations. This opens the door to quantifying the influence of prior knowledge on the probability of misidentification.

What Happens When You Profit from Prior Knowledge

One of the outcomes of our analysis is that the misidentification probability naturally splits into two components:

• a prior effect, coming from how strongly the prior separates promising from unpromising configurations, and
• a sampling effect, coming from the data we collect.

If the prior is informative, it exponentially suppresses suboptimal arms and reduces the sample budget needed to identify an ϵ-best configuration. If the prior is uninformative, or even misleading, our bounds show that the algorithm simply transitions back to the behavior of standard, prior-free methods. This ensures robustness, which we found essential for practical use.

Incorporating Theory into our Algorithm

To bring these insights into HPO, we introduce Prior-Guided Successive Halving (PSH). It builds on classical Successive Halving but incorporates two key elements:

• Gaussian process models for learning-curve extrapolation, and
• a theoretically grounded early-stopping rule derived directly from our bounds.

In every round, PSH updates posterior predictions for the remaining configurations and checks whether the current evidence—prior plus observations—is sufficient to guarantee with high probability that the leading configuration is ϵ-optimal. When that happens, the algorithm stops immediately, saving potentially large amounts of evaluation budget.

How PSH Compares to Standard Successive Halving

A key takeaway from our comparison is that informative priors allow us to relax the traditional 𝑂(Δ−2)O(Δ−2) dependence on performance gaps that standard SH suffers from.

• With useful priors, PSH requires significantly fewer evaluations.
• With uniform priors, PSH behaves almost exactly like SH.
• With misleading priors, PSH incurs only a bounded overhead and never exceeds the original SH budget.

In other words, prior knowledge helps when it should, and gracefully steps aside when it shouldn’t.

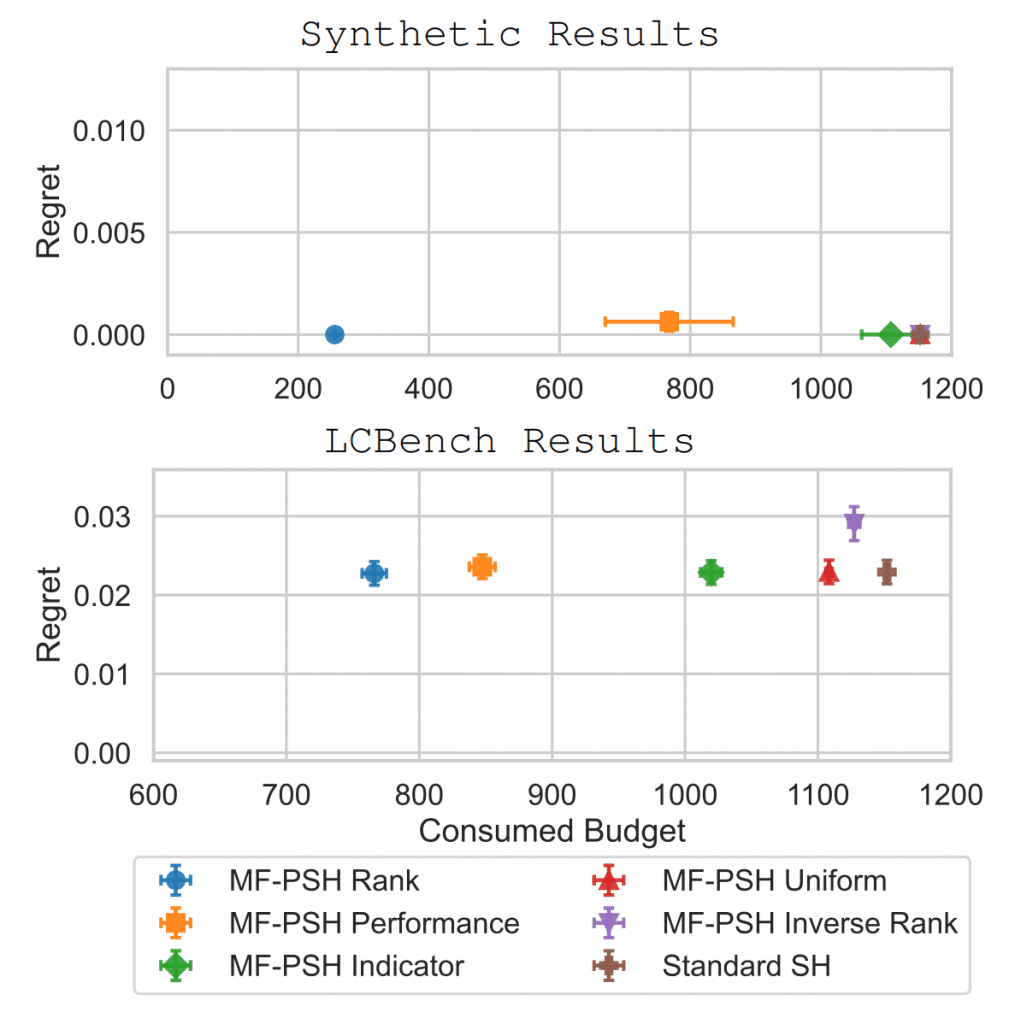
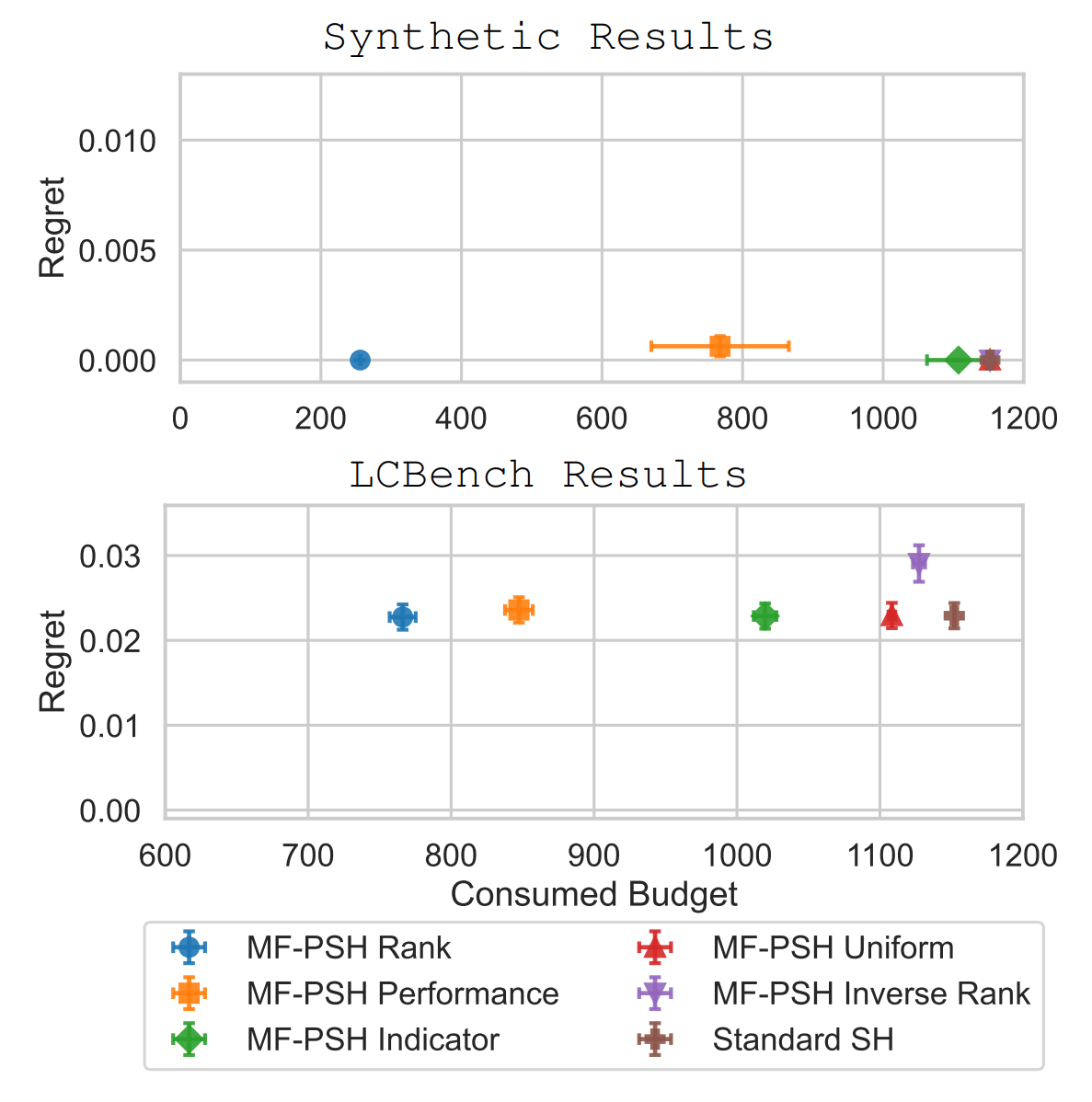
What We Saw in Practice

Our experiments on a synthetic benchmark and on LCBench illustrate the theoretical behavior clearly. Rank-based and performance-based priors led to substantial reductions in evaluation budget, by the order of 80–90% on the synthetic task and around 35% on LCBench, without affecting regret.
Uniform priors produced almost identical behavior to standard SH, as predicted. Even adversarial priors were overridden quickly through GP-based learning-curve updates, highlighting the robustness we aimed for.

In summary, our paper provides a formal, distribution-dependent characterization of how prior knowledge influences sample complexity in multi-fidelity HPO. The Prior-Guided Successive Halving algorithm translates these findings into a practical method that can substantially reduce evaluation cost while maintaining reliability.
We see this as a step toward more compute-efficient and sustainable AutoML, where prior knowledge is not just an informal boost but a mathematically grounded tool for reducing resource consumption.